
June, 2022

Stability is the property of a system to be resilient to disturbance and return to its original state or behavior. For max-plus-linear systems, stability of their operation can be related to the maximum throughput that they can sustain. Intuitively, if the system operates at maximum throughput there is no room, no slack, to recover from any disturbance to its operation. Disturbances could be incidental late arrival of inputs, or incidental extension of the duration of an operation. As in the unstable manufacturing system shown in Figure 35, the disturbance from the nominal schedule diverges and the operation fails.
A max-plus-linear system is called stable under infinite input sequences \(i_1, \ldots{}, i_k\) if for any finite disturbance to an input sequence, only a finite number of output events change.
Let \(i\mathbin{\stackrel{S}{\longrightarrow}} o\) be the behavior of a max-plus-linear event system \(S\) with input \(i\). \(S\) is called stable under input \(i\) if for any \(c\in{}\mathbb{T}\), \(k\in{}\mathbb{N}\), and \(i\oplus{}c\otimes{}\delta{}^{k}\mathbin{\stackrel{S}{\longrightarrow}} o'\), there is some \(m\in{}\mathbb{N}\) such that for all \(n\in{}\mathbb{N}\), \(n\geq{}m\), if \(o(n)\) is defined, then \(o'(n)=o(n)\).
The definition is straightforwardly generalized to systems with multiple inputs and outputs by requiring that a disturbance on any of the inputs influences only a finite number of output events on all outputs.
Note that if \(o\) is finite the system is trivially stable under input \(i\).
We consider the conveyor belt as a max-plus-linear event system as in Example 9, \(i\mathbin{\stackrel{CB}{\longrightarrow}}o\), with inputs \(i=[0,0,2,2,4,4,\ldots{}]\) and corresponding outputs \(o=[5,6,7,8,9,10,\ldots{}]\). This represents an unstable situation, for there is a finite disturbance on the input that will disturb an infinite number of outputs. An example of such a finite disturbance is \(4\otimes\delta{}^2\), which, when added to \(i\) gives the input \(i_d=[0,0,4,2,4,4,\ldots{}]\) with corresponding output \(o_d=[5,6,9,10,11,12,\ldots{}]\) and \(o_d(k)\neq{}o(k)\) for all \(k\geq{}2\).
A stable operation, on the other hand, of the conveyor belt is obtained by replacing the input with \(i'=[0,0,3,3,6,6,\ldots{}]\). In this case, \(o'=[5,6,8,9,11,12,\ldots{}]\). When the same disturbance is applied we get \(i'_d=[0,0,4,3,6,6,\ldots{}]\) and \(o'_d=[5,6,9,10,11,12,\ldots{}]\) and \(o'_d(k)\neq{}o'(k)\) only for \(k=2,3\). In this case, any finite disturbance influences only a finite number of outputs.
Operating the conveyor belt at the maximum throughput makes it unstable. Lowering the rate of inputs, as in the second case, makes it stable.
The following gives a sufficient condition for stability of a max-plus-linear event system.
Let \(S\) be a max-plus-linear and index-invariant system with maximal throughput \(\tau{}(S)\). \(S\) is stable under inputs \(i_1\ldots{}i_k\) if for all \(k\) \[\tau{}(i_k) < \tau{}(S)\]
We can also apply the concept of stability to a schedule for a max-plus-linear system given in its state-space representation. A max-plus-linear system is called stable under schedule \({\bf{\sigma{}}}(k)\) and inputs \({\textrm{\bf{}{u}}}(k)\) if for a finite disturbance to the \({\textrm{\bf{}{u}}}(k)\) only a finite number of changes happen to the execution \({\textrm{\bf{}{x}}}\) under \({\bf{\sigma{}}}(k)\), i.e., there are only a finite number of changes to the state vectors and to the output vectors.
Let \(S\) be a linear event system with \(n\) inputs in state-space representation. Let \(S\) be executed according to schedule \({\bf{\sigma{}}}(k)\) resulting in the sequence \({\textrm{\bf{}{x}}}(k)\) of state vectors and the sequence \({\textrm{\bf{}{y}}}(k)\) of output vectors. \({\bf{\sigma{}}}(k)\) is called stable for \(S\) under input \({\textrm{\bf{}{u}}}(k)\) if for any \({\textrm{\bf{}{c}}}\in{}\mathbb{T}^n\) and \(m\in{}\mathbb{N}\), the execution with schedule \({\bf{\sigma{}}}(k)\) and inputs \({\textrm{\bf{}{u}}}'\) with \({\textrm{\bf{}{u}}}'(m)={\textrm{\bf{}{u}}}(m)\oplus{}{\textrm{\bf{}{c}}}\) and \({\textrm{\bf{}{u}}}'(k)={\textrm{\bf{}{u}}}(k)\) for \(k\neq{}m\), leads to a sequence \({\textrm{\bf{}{x}}}'(k)\) of state vectors and a sequence \({\textrm{\bf{}{y}}}'(k)\) of output vectors, such that there is some \(l\in{}\mathbb{N}\) such that for all \(k\in{}\mathbb{N}\), \(k\geq{}l\), \({\textrm{\bf{}{x}}}'(k)={\textrm{\bf{}{x}}}(k)\) and \({\textrm{\bf{}{y}}}'(k)={\textrm{\bf{}{y}}}(k)\).
In Example 23, we have seen that the fastest train schedule can repeat every 4 hours. The schedule is shown in Figure 27. The schedule assumes that all trains arriving from Liège, the inputs to the system, are in time for the schedule to be valid.
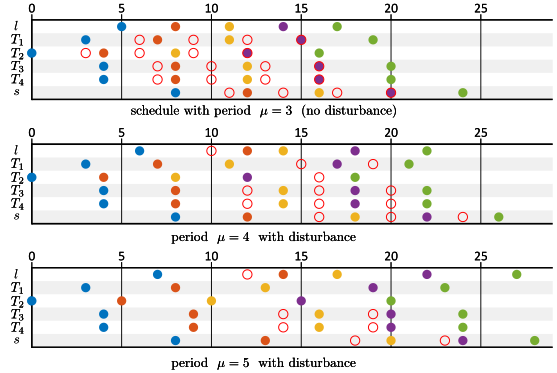
Any schedule with a period smaller than four is unstable (and not valid, according to Definition 35). The first sequence in Figure 36 shows a schedule \({\bf{\sigma{}}}_3\) with period three and the actual sequences according to the execution. Deviations between schedule and actual execution are shown in the figure by red open circles denoting the scheduled time stamps and the filled circles denoting the actual time stamps on those events that do not occur according to their original schedule.The figure shows that the schedule cannot be followed and the deviation from the schedule increases with subsequent iterations. We say that the schedule is unstable.
The second sequence shows execution according to a periodic schedule \({\bf{\sigma{}}}_4\) with period four, i.e., equal to the largest eigenvalue of the state matrix. This situation is called marginally stable since disturbances that occur, neither dissolve nor diverge. It is unstable according to Definition 40. A disturbance is introduced in the sequence by the second train from Liège arriving two hours late. As a consequence the execution deviates from the schedule (by two hours) and this deviation remains present in all future states and outputs.
Now assume that we introduce some slack in the schedule and we operate at a period of 5 hours instead of 4. This is shown in the third sequence with schedule \({\bf{\sigma{}}}_5\). Again, a disturbance is introduced by the second train being late by two hours. This time, the system is stable. The disturbance diminishes with subsequent iterations. For example, the third train to Schiphol is late by two hours, the fourth train is still late, but only by one hour and the following trains are on time again.
A valid schedule is stable if the throughput it requires from the system is lower than the maximal throughput the system can sustain.
Let \(S\) be a max-plus-linear system in state-space representation with state matrix \({\textrm{\bf{}{A}}}\). Let \(\lambda{}\) be the largest eigenvalue of \({\textrm{\bf{}{A}}}\). Let \({\bf{\sigma{}}}\) be a valid schedule for \(S\) under inputs \({\textrm{\bf{}{u}}}(k)\). Then \({\bf{\sigma{}}}\) is stable for \(S\) under inputs \({\textrm{\bf{}{u}}}(k)\) if the throughput of the event sequences for each of the state elements in \({\bf{\sigma{}}}(k)\) are smaller than \(\frac{1}{\lambda{}}\).
Reconsider the wireless channel decoder and its state-space model of Exercise 19.